Friction Theories
Friction is the resistance to relative motion, which is experienced whenever one solid body slides over another. The resistive force, which is parallel to the direction of motion, is called the friction force. If the solid bodies are loaded together and a tangential force is applied, then the value of the tangential force, which is required to initiate sliding, is the static friction force. The tangential force required to maintain sliding is the kinetic friction force. Kinetic friction is generally lower than static friction.
The Laws of Friction:
First law states that the friction is independent of the apparent area of contact between the contacting bodies.
Second law states that the friction force is proportional to the normal load between the contacting bodies.
Third law states that the kinetic friction is nearly independent of the speed of sliding.
First two laws are often referred to as Amontons laws and Coulomb introduced third law.
Coefficient of Friction:
The second law states that the friction force F is proportional to the normal load W.
i.e., F α W
Therefore F = m W
Where m is a constant known as the coefficient of friction and is a constant only for a given pair of sliding materials under a given set of ambient conditions and varies for different materials and conditions
We know that nearly all surfaces are rough on a microscopic scale and real contact is obtained over a small fraction of the apparent contact area. Thus the real area of contact is independent of the apparent area of contact so the first law of friction is explained that friction is related to the real area of contact and independent of the apparent area of contact.
Friction Measuring Devices:
Any apparatus for measuring friction must be capable of supplying relative motion between two specimens, of applying a measurable normal load and of measuring the tangential resistance to motion. Commonly used devices are pin on cylinder or disk and disc on disc. In these cases, one specimen, usually a disc or a cylinder is driven continuously while a second specimen nominally stationary, is loaded against it.
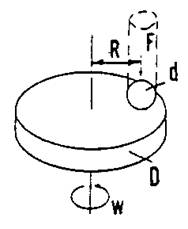
Figure: Schematic of pin-on-disk test system.
Causes of Friction:
When two surfaces are loaded together they can adhere over some part of the contact and this adhesion is therefore one form of surface interaction causing friction. If no adhesion takes place then the only alternative interaction which results in a resistance to motion is one in which material must be deformed and displaced to accommodate the relative motion. We can consider two types of interaction
1. Asperity interlocking - motion cannot take place without deformation of the asperities.
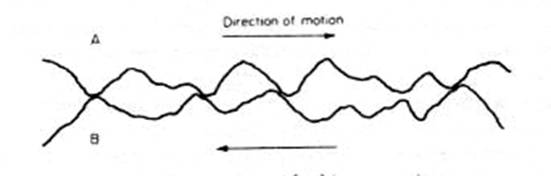
2. Macro displacement Here a hard sphere A loaded against a softer B causes displacement of material B during motion.

So we have two types of interaction
1. Adhesion
2. Material displacement - either due to asperity interlocking or macro displacement
Adhesion
Theory of Friction:
Bowden and Tabor explained the adhesion theory of friction when metal surfaces are loaded against each other, they make contact only at the tips of the asperities. Because the real contact area is small the pressure over the contacting asperities is assumed high enough to cause them to deform plastically. This plastic flow of the contacts causes an increase in the area of contact until the real area of contact is just sufficient to support the load. Under these conditions for on ideal elastic-plastic material
W = A .
Where A is the real area of contact and
When the metals are in contact, cold welding takes place due to adhesion. So a force S per unit area of contact necessary to shear the junction
F = A.S + Pe
Where Pe is the force required to plough hard asperities through a softer surface. For most situations involving unlubricated metals Pe is small compared to AS and may be neglected.
Therefore, F = AS
F = (W/
F/W = S/
Therefore m = F/W = S/
Thus this theory explains two laws of friction
· The friction is independent of the apparent area of contact and
· Friction force is proportional to the load
For most metals
S=
So adhesion theory predicts that m = 0.2, when the material pairs are similar. It should be true for any combination of same material. But it is not true usually because of junction growth and work hardening.
The above theory is true for static contacts. But when tangential force is applied, yielding takes place as a result of the combined normal and shear stresses. So Bowder and Tabor re-examine some of the assumptions and present a modified description of friction as
A2 = (W/Po)2 + a (F/Po)2
Where the W/Po is the area of contact derived from the above theory in which only the effect of normal load is considered and the additional term a (F/Po)2 represents the increase caused by the shear or friction force.
High values of friction are obtained for metal under high vacuum condition, where adhesion is unimpeded by oxide film or other contaminants, indicates larger real contact area.
Criticisms of Bowden and Tabor Theory of Friction:
1. m is not always 0.2 when similar metal slid over each other.
2. No normal component of friction is detected. i.e., to measure adhesion in the normal direction, the normal load must first be released and elastic recovery will break many of the bonds during this process.
3. Formation of loose wear particles is not explained. i.e., Most of the experiments have done in single pass. So single pass experiments not necessarily produce loose wear particles.
4. The area of contact is always proportional to the initial plastic strain.
Plowing Effect
Plowing caused by asperities of a hard metal penetrating into a softer metal and plowing out a groove by plastic flow in the softer material. This is a major component of friction during abrasion processes and also it is probably important in cases where the adhesion term is small.
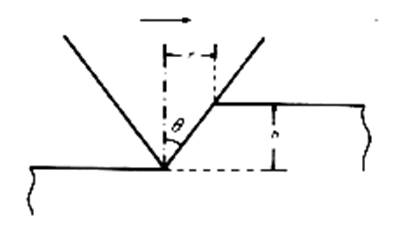
Figure shows the plowing of a soft surface by a hard conical asperity
Consider a hard material whose surface is composed of a large number of similar conical asperities of semi-angle q in contact with a softer material whose surface is comparately flat. During rubbing only the front surface of each conical asperity is in contact with the opposing material and the vertically projected area of contact is given by
A = n . (1/2) . p . r2
Where n is the total number of asperities.
We know that
W = A .
W = n . (1/2) .
p
. r2 .
The friction force F is obtained in a similar manner by considering the total projected area of material, which is being displaced by plastic flow, that is
F =
n . r. h .
Therefore, m = F/W = 2h / pr
But h/r = cot q
Therefore, m = (2/p). cot q
Using this approach, m always equal to one half the vertical projected area of the asperity divided by the horizontal projected area of the asperity. The above theory assumes that the yield pressure is the same in the vertical and horizontal direction
Bowden and Tabor states that the contribution of ploughing to friction is small for the following reasons. The tangential resistance to sliding for a single asperity is made up of a shear term and a ploughing term
F = AV . So +
AH .
Where Av and AH are the vertical and horizontal projected areas.
For asperities on most metal surfaces, the angle q is large and AV / AH is very small, so that the ploughing term is negligible in comparison with the adhesion term. For rough surfaces where q is larger, the ploughing term can be comparable to the adhesion term.