Genesis and mechanism of friction

Introduction

One of the fundamental aspects of friction is genesis of friction that is force generation and transmission between the surfaces in contact. The genesis of friction is the most important energy consuming mechanism than other interfacial considerations. Right from Amonton (1699) to Bowden (1930s) and Tabor (1950) have proposed many theories to explain friction. Among these friction theory dominated all others over many decades. But the large variations in the experimental values and calculated values have not been solely explained by adhesion theory. The more realistic model is explained in terms of three different mechanisms by Nam. P. Suh and H. C. Sin (1981). Those are namely adhesion, asperity deformation and plowing.

The frictional force depends on the history of sliding. Frictional force undergoes significant variation during the early stages of sliding before it reaching steady state. This behavior is important in tribology not only because of frictional force and also of generic effect on wear. To explain the genesis of friction Nam.P. Suh and H, C. Sin have done a set of experiments and those detail given below briefly.

Testing and experimental observations

Testing method adopted was cross cylinder geometry with one stationary and other moving. The parameters were 1kg normal load, 0.02m/s-sliding rate for total of 32 m length at room temperature. The test was carried out in argon atmosphere and the normal and fractional force was measure by dynamometer recorder assembly. The materials taken for the testing were Arco Iron, AISI 1020, 1045, and 1095. and also OHFC copper polished up to 4/0 slid against AISI 1020 steel. Out of the results following two points are important

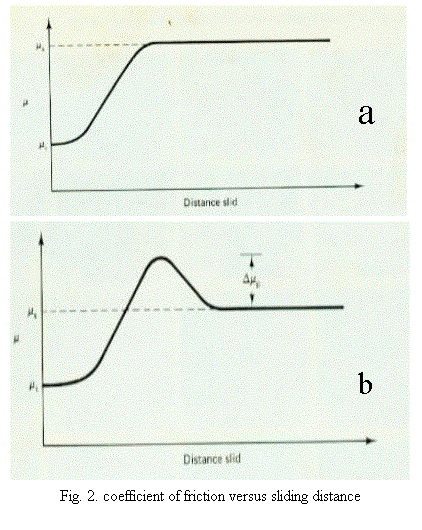
·        Coefficient of friction changes as a function of sliding distance at early stages. It has usually low value and increases gradually until reaching the steady state. After reaching the maximum value some times coefficient of friction decreases to the steady state if the stationary slider is harder than the moving specimen. The same pair of specimen does not show such a result when those are reversed. The initial value of coefficient of friction observed was 0.1 to 0.2 regardless of the materials..

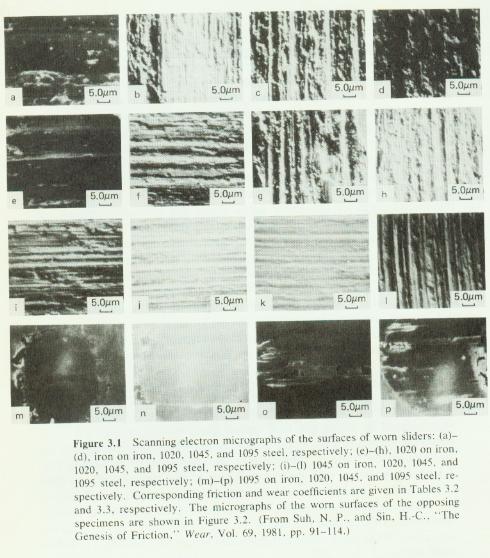
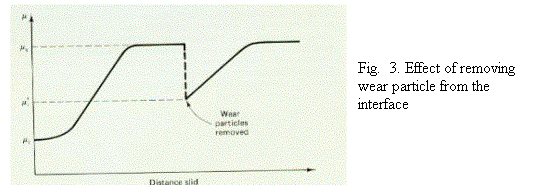
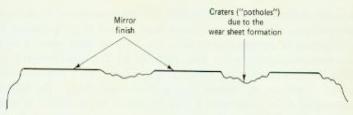
·        Steady state coefficient of friction and wear rate higher when identical metals are slid against each other than harder stationary slider slid against softer specimen. Where as the coefficient of friction in softer stationary slider slid against hard moving specimens as identical specimen. In this case wear is much higher in different material sliding. This behavior related to the SEM photographs worn out surfaces. These figures shows that when harder stationary slider slid against softer moving specimens, harder specimen gets mirror polishing and the material underneath the mirror polished surface fails and forms the new asperities and those gets mirror polish and so on. But this does not happen for the reverse combination and identical materials because softer surface wear continuously. The wear particles gets entrapped in-between the surfaces and many plowing surfaces are seen in the topography.

The experimental observations made out of the results

• The coefficient of friction vs. sliding distance may be summarized by using the two typical plots fig.2  a and b. The behavior shown in fig.2 always holds when identical metals slid against each other and the behavior shown in fig.3 characteristic of mirror polishing of harder specimen when it is stationary.

• When the wear particles are brushed from the sliding surfaces, coefficient of friction decrease to a value and gradually reach the steady state again. which given by the fig.3

• Coefficient of friction can differ as much as 0.2, even the same pair of chemically identical materials, depending on which is stationary and moving one.

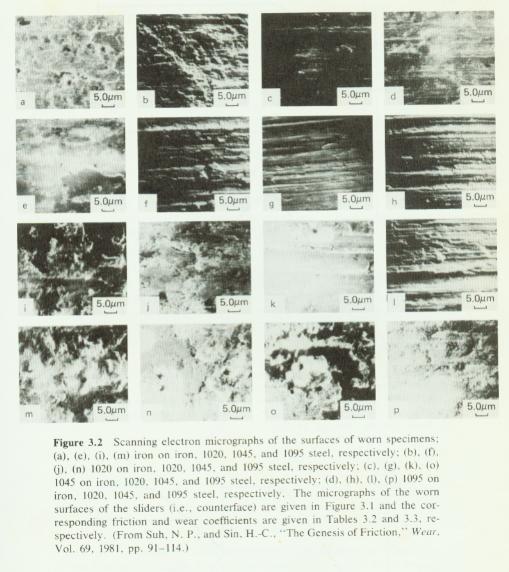
·        The initial value of coefficient of friction observed was 0.1 to 0.2 regardless of the materials and weather lubricant is used or not.( for Au-Au, Cu-steel and Brass –steel)

• When the sliding test performed with highly polished surface plowing grooves formed from the onset of testing.
• Frictional behavior depends very much on experimental conditions.

Genesis of friction

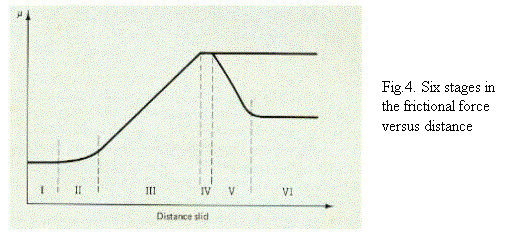Out of the experimental results one can understand coefficient of friction cannot be explained solely by adhesion theory. So the friction coefficient is the combined effect of asperity deformation (μ_d), plowing by wear particles (μ_p) and adhesion between the flat surfaces (μ_a).. to clarify the time dependant frictional behavior of the material tested., the plot of friction vs.  sliding distance will be subdivided into six sages as show in fig.4

Stage 1

• Frictional force is largely depends on the plowing of surface by asperities
• Adhesion does not play any role due to contaminated nature of the surface.
• Asperity deformation does take place, which affects the static coefficient of friction, but it is not a major factor
•  The coefficient of friction in the initial stage (μ_i ) depends on material combination, surface condition and environmental conditions.

Stage 2

• Slowly slop begins to rise, if the surface is lubricated stage 1 persists for long time and stage 2 may not be present
• The slope can be steeper if the wear particle generated by the asperity deformation and fracture entrapped between the surfaces and plow the surfaces.

Stage 3

• Steep rise in slop due to rapid increase in wear particles, adhesion due to clean contact between the surfaces and force required to deform the surface.
• Wear particles are generated due to the sub surface deformation, crack nucleation and crack propagation (delamination theory).
•  Plowing will be the greatest effect on the friction coefficient when the wear particle entrapped between the identical materials.

Stage 4

• This stage occurs when the number of entrapped particles equal to the number of leaving particles from the surface.
• Adhesion contribution remains constant.
• Asperity deformation also contributes due the deformation of newly formed asperities.
• When identical metals sliding each other this stage remains constant and mechanism for the fifth stage does not exits.

		Fig.5. Hard stationarysurface polished by soft surface

 

Stage 5

• When hard stationary slider slid against soft specimen, hard specimen asperities get mirror polished as shown in the fig.5
• In this case frictional force decreases due to reduction in plowing and asperity deformation effect.

Stage 6

• Both the surfaces get mirror finish but always there are some potholes due to the delamination wear particles. Therefore the surfaces never completely smooth.
• These potholes provide anchoring points for wear particles.
• When the stationary slider is not harder the surfaces remains rough and stage 5 and 6 will not present

Friction generating mechanisms

1.      Asperity deformation

2.      Plowing

3.      Adhesion

Asperity deformation determines the static coefficient of friction and also affects the dynamic coefficient of friction. But contribution is less than plowing and adhesion.

Asperity deformation friction coefficient (μ_d)

Consider two asperities coming to contact with each other, they have to deform in a manner that the resulting displacement field is compactable with sliding direction and that the sum of vertical components of the surface traction at the contacting asperities must be equal to the normal applied load. Consider the following diagram, the solution demand that shear stress along OA be what ever is necessary to satisfy the condition that

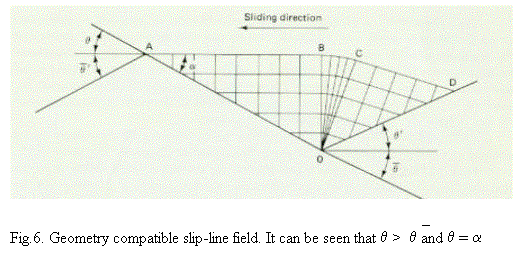
q = a ,  which is necessary to constrain the deformation to the sliding direction. This would be possible even under the lubricated condition if the inter OA not perfectly smooth enough to cause mechanical interlocking. The general solution ( m_d = tan q ) s sketched in the following figure.

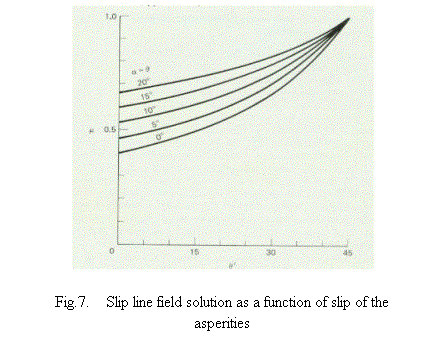
 If it is assumed that the asperity deformation is the only phenomenon that takes place at the interface and is entirely responsible for the frictional force under a given load, the coefficient of friction due to asperity deformation various from 0.39 – 1 as the slope of the asperity increases from 0 – 45^o. These values are closer to the static coefficient of friction. This is well suited for the  rough surfaces as like identical specimens slid each other.

Adhesion component of friction coefficient (μ_a)

• A frictional can arise due to the adhesion of two nearly flat surfaces. It happens due to either welding of two nearly flat portions or when the atoms brought together in close proximity for inter atomic distances with out welding.
• Due to contaminated nature if the surface at initial stages of the sliding μ_a is negligible.
• Due to the deformation of the asperities exposure to the new fresh surface may increase the adhesion component

Consider two nearly flat surfaces coming into contact (rubbing contact) as shown in fig.8. Depending on the nature of adhesion along the interface ED, the required to move the rubbing surface with respect to each other varies. When there e is no adhesion force required is zero and it is maximum when there is complete adhesion.

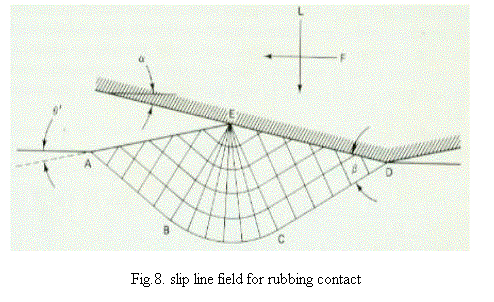
Solution has been derived based on the slip line field is give below

                      μ_a=  [A sin α + cos (cos^-1f - α)]  /  [(A cos α + sin (cos^-1f – α)]

Where

                     A = 1 + π/2 + cos^-1f - 2α – 2sin^-1{sin α /(1-f) ^½}

f - strength of adhesion at ED as expressed as the fraction of
     shear flow strength  of the soft material.

α – slope of the hard asperity

for nearly flat surfaces α tends to 0, therefore

                             μ_a= f / (A + sin (cos^-1f – α)

Where

A = 1 + π/2 + cos^-1f

μ_a various from 0 to 0.39 as f changes to 0 to 1.   the friction force calculated by the above formula is based on the assumption that all the load applied is carried by the flat surfaces. Under the typical condition μ_a should be less than 0.4 but the experimental result of hard stationary slider slid against soft specimen shows that the steady state value of 0.51 when both surfaces polished smoothly. This result conforms the contribution of asperity deformation and plowing component.

Plowing component of friction coefficient (μ_p)

• The plowing component of the frictional force can be due to the penetration of hard asperities or due to the penetration of the wear particles. The plowing due to the wear particle is illustrated in the following figure.

• As the surface move with each other, groove will be formed in one or both the surfaces depends on the material, plowing will occur on the soft surface.
• When the hard surface is very rough, wear particles can anchor in the hard surface and plow the soft surface
• Plowing component is very sensitive to ratio of the radius of curvature to the depth of penetration. The friction coefficient by plowing  μ_p is given by

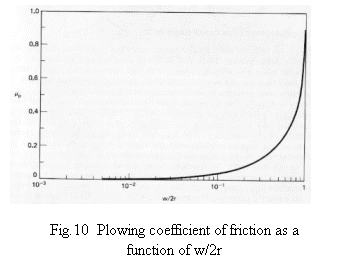
μ_{p =} 2/π { (2r/w)² sin ^–1(w/2r) – [(2r/w) - 1]^1/2 }

where w is width of penetration and  r is radius of curvature of the particle.

• The ratio can be measured by cutting the worn out surface and see it in the SEM. This value found to be nearly 0.8 and substituting to the equation plowing coefficient of friction found to be 0.2
• This value is equal to the reduction in friction when the wear particle are removed from the interface
• Plowing coefficient of friction as a function of w/2r is shown in the figure followed

• Friction not only increases the fictional force and delamination wear, and also increases the small wear particles, which in turn affect the wear of sliding surface.
• Plowing action forms ridges along the side of plowed groove. This ridges produces the ear particle under the repeated loading

Other friction components

• When the visco-elastic elastic surfaces with high hysteresis loss are slid against each other, the external work must be done by the tangential component of the surface traction to over come the cyclic energy loss due to the hysteresis loss. This energy loss shall be added to the frictional force.
• When wear debris stick to the surface that will under go repeated plastic deformation this will increase the frictional force. E.g. graphite reinforced polyurethane sliding against steel surface  
• Frictional force is a result of work done a the interface. Therefore, any any consuming mechanism exist between and near the interface will be added to the frictional force.

References

1.      Nam P. Suh, Tribophysics, Prentice Hall, INC, New Jersey ,1986

2.      Nam P. Suh and H. C. Sin, The Genesis of friction, Wear, 1981, 91-114