Submitted by
Mohan Kulkarni
Souvik Math
(To be verified)
HYDRODYNAMIC LUBRICATION :
Pumping Action
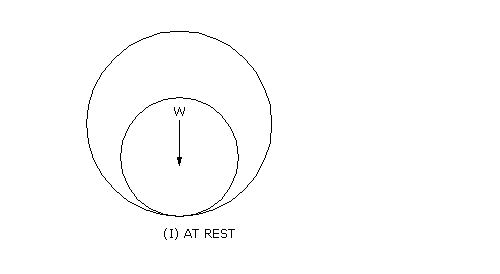
When dry, friction will cause the journal to try to climb
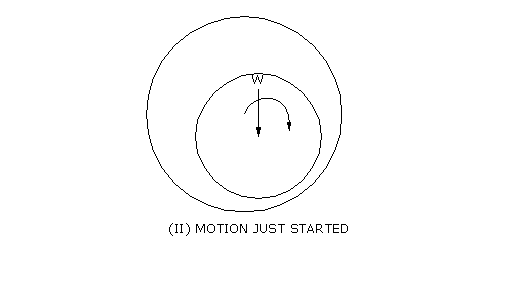
bearing inner wall(FIG 1).When lubricant is introduced, the —climbing action
(FIG II) and the viscosity of the fluid will cause lubricant to be drawn
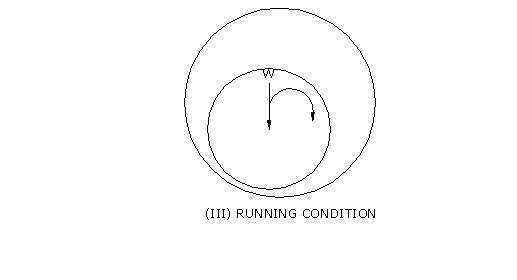
around the journal creating a film between the journal and bearing .The
lubricant pressure will push the journal to the other side of the bearing (FIG
III). The pressure is developed because of the converging wedge formed between
the journal and the bearing.
Assumptions made in
deriving the Reynold’s equation:
- Body forces are neglected, which means that there is no
outside field of force acting on the lubricant, such as -- gravitational or
magnetic forces etc. This is not true if magnetic and electric fields play a
part such as in magneto hydrodynamics.
- The pressure is considered to be constant through out
the thickness of the film. As the oil film is very thin of the order of a few
thousands of an inch at most, the pressure can not vary significantly across
it. When the elastic properties of the lubricant are considered that may not
hold, but no work has demonstrated that with normal fluids this assumption is
invalid.
- The curvatures of the bearing surfaces are considered to
large compared with the oil film thickness. The surface velocities need not
therefore be taken as varying in direction.
- There is no slip at boundaries, which means that the
velocity of the surface is the same as the velocity of the lubricant in
contact with the surface.
- The lubricant obeys Newton’s law of viscosity
- Flow is laminar. This is true with bearings of normal
dimensions and speeds, but in cases of large journals with high speeds the
flow is turbulent.
- The fluid inertia can be neglected. It has been observed
that even at higher Reynold’s no. of 1000 or so, the pressures are only
modified by about 5%, if inertia is considered.
- Viscosity of the lubricant is taken as constant through
out the thickness of the film. This assumption is made for mathematical
simplicity
- There is no flow in Z i. e. axial direction of the
bearing.
Derivation of the
Reynold’s equation:
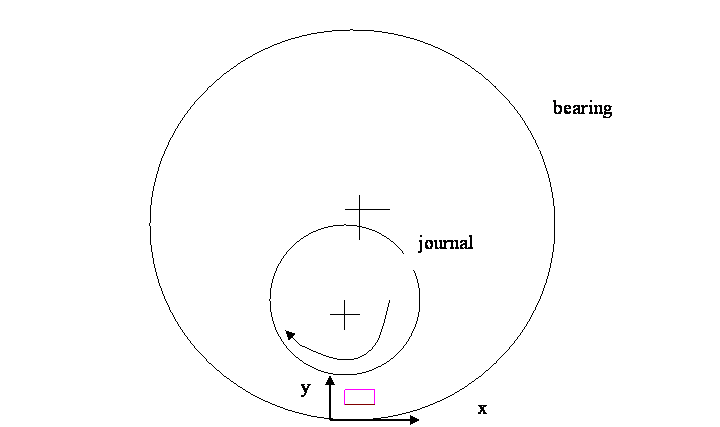
The
coloured rectangular area from the figure above is zoomed and its 3D view is
taken below for force calculation :

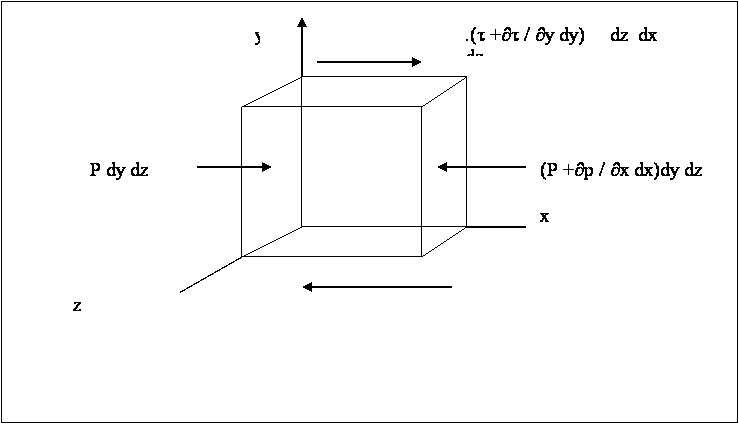
From force equilibrium we get
∂p / ∂x = ∂τ / ∂y
……………. (1)
From Newton’s law of viscosity
. τ = µ ∂u / ∂y
from eqn . (1) we get
∂p / ∂x = µ ∂ 2u /
∂y2 ……………..(2)
∂p / ∂x = ( dp / dx) ; as
pressure is not varying in y and z direction.
∂ 2u / ∂y2 =
1/ µ ( dp / dx)
Integrating
u = 1/ µ ( dp / dx) y2
/2 + C1 y + C2
putting boundary conditions
At y = 0, u = 0
C2
= 0
At y = h , u = - U
C1
= - U / h – h / 2 µ ( dp / dx)
u = 1/ µ (
dp / dx) y2 /2 –{ U / h – h / 2 µ ( dp / dx)}y
Flow Rate Q =
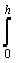 u dy
u dy
= - Uh/2 - { (h 3 /12µ )( dp / dx)}
Considering
the flow to be incompressible ,
. dQ/ dx
= 0
hence,
- U/ 2 ( dh /dx ) - d / dx { (h 3 /12 µ )( dp / dx) } =0
so
d /
dx { ( h 3 / µ )( dp / dx)} = - 6 U ( dh /dx )








![]() u dy
u dy