Tutorial 1
- An Inertial slider is a friction based drive used in
AFMs and is a promising drive for MEMS. One version of the drive is as shown
in the figure
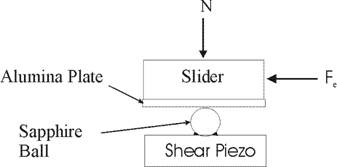
Write down the equation of
motion for the slider considering the friction between the sapphire ball and
alumina plate? What are the conditions for,
- Sapphire and alumina to stick and move as one unit?
- Sapphire slips against alumina?
Assume what ever you need as a
practical engineer would do.
If a quadratic voltage pulse
followed by sharp drop to zero voltage is applied between the top and bottom
face of the piezo, trace the displacement of the slider. (Displacement of the
piezo = d51 Voltage; d51 = 1 nm/volt )
- The surface roughness can be modeled as a fractal using
the Weierstrass-Mandelbrot Function,
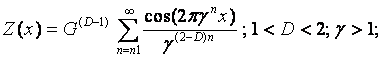
G is a scaling constant and D is
the fractal dimension and 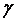 = 1/λ is the frequency mode corresponding to the reciprocal of
the wavelength (λ) of roughness and nl is the lower cut off frequency and upper
summation limit can be cut off to nh a higher cutoff frequency.
= 1/λ is the frequency mode corresponding to the reciprocal of
the wavelength (λ) of roughness and nl is the lower cut off frequency and upper
summation limit can be cut off to nh a higher cutoff frequency.
Derive the traditional roughness
parameters like Ra, Rz etc from the above equation.
Can you simulate a surface
profile numerically using the above function?
- Derive the constants a and b of the Leonard Jones
potential (given by V=-a/r6 + b/r12) as a function the
experimentally determinable parameters (like the Elastic modulus and
equilibrium inter-atomic distance r0 )
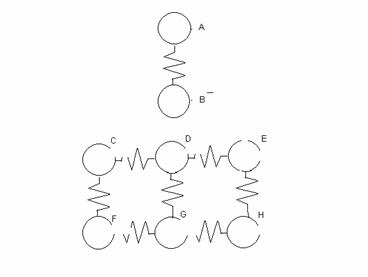
- Assuming that the atoms in the metal can be modeled as
spring and mass system derive the coefficient of friction between two atoms as
shown in figure. The Spring stiffness can be assumed as E/ro. E –
elastic modulus and ro The equilibrium distance between atoms.
Assume Leonard jones potential between atoms B and D and that there is no
interaction between B and C And B and D.


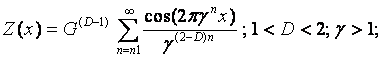
![]() = 1/λ is the frequency mode corresponding to the reciprocal of
the wavelength (λ) of roughness and nl is the lower cut off frequency and upper
summation limit can be cut off to nh a higher cutoff frequency.
= 1/λ is the frequency mode corresponding to the reciprocal of
the wavelength (λ) of roughness and nl is the lower cut off frequency and upper
summation limit can be cut off to nh a higher cutoff frequency. 