Minimize f = (5/x1) + (2/x2)
with respect to {x1, x2}
Subject to
g1 = x1 + x2 - 3 <= 0
g2 = 4x1 + x2 - 6 <= 0
g3 = x1 + 3x2 - 20 <= 0
-x1 <= 0 and -x2 <= 0
"<=" indicates "less than or equal to". [From p. 249 of "Numerical Optimization Techniques for Engineering Design" by G. N. Vanderplaats, McGraw-Hill, New York, 1984]
Solve the above problem by hand and by using Matlab's fmincon routine. Draw the contours of the objective function, the curves of the constraints, and show the feasible space in a 2D plot. Indicate the optimum in the figure. Show what paths the algorithm takes to reach the optimum from different initial guesses.
As shown in Fig. 1, a farmer needs to decide the boundary of his farm between the river and the three roads to enclose an area A He wants to minimize the length of the fence (excluding the roads) that separates his farm from the river. The animatation in Fig. 1 shows that the farmer is not able to decide the bondary curve. Help him determine the boundary curve using the following information.
- The origin is at the bottom-left corner of the green patch. Let the right edge of the left vertical road be the y-axis and the top edge of the horizontal road be the x-axis.
- The horizontal extent between the two vertical roads (i.e., along the x-axis) of the green patch is 10 m.
- The equation of the lower boundary of the river is given by (-0.8x + 8 = y). Note that this is different from what is shown in Fig. 1.
- The farmer is allowed an area of 25 m2 (i.e., A = 25 m2).
- What changes if the farmer is allowed 35 m2 (i.e., A = 25 m2)?
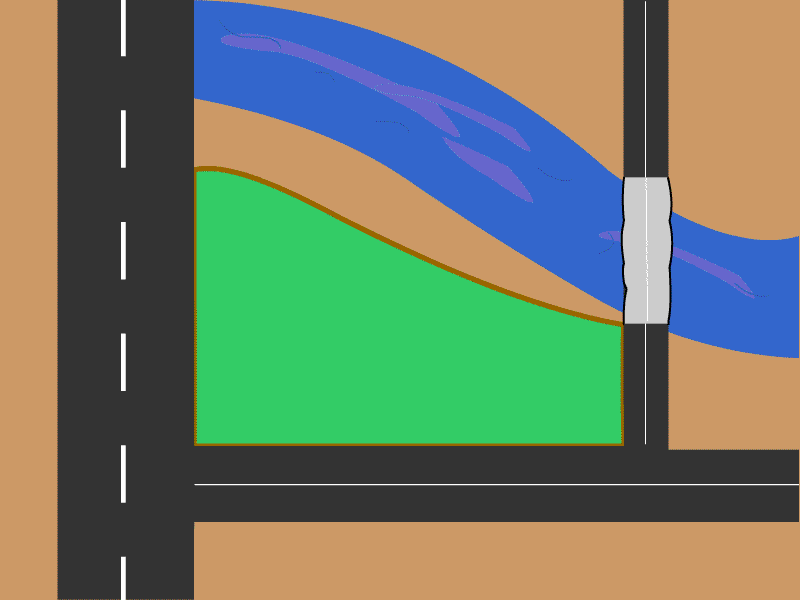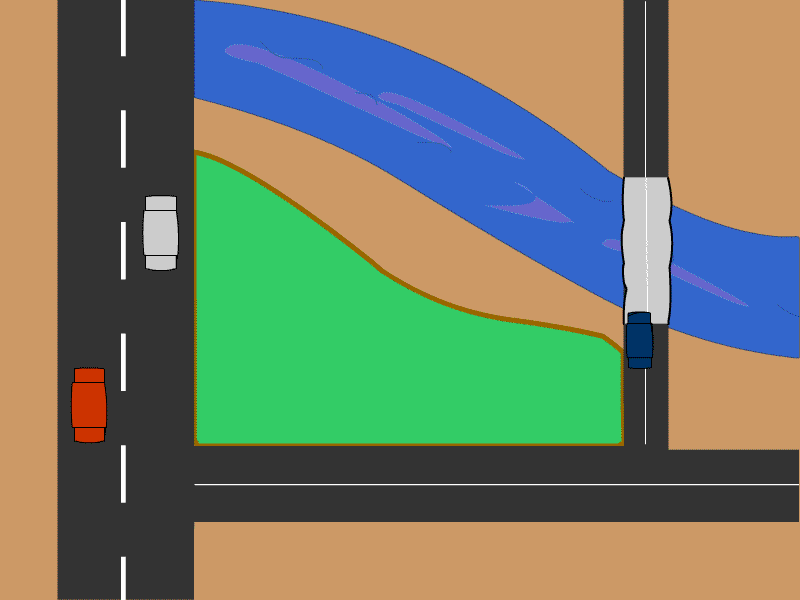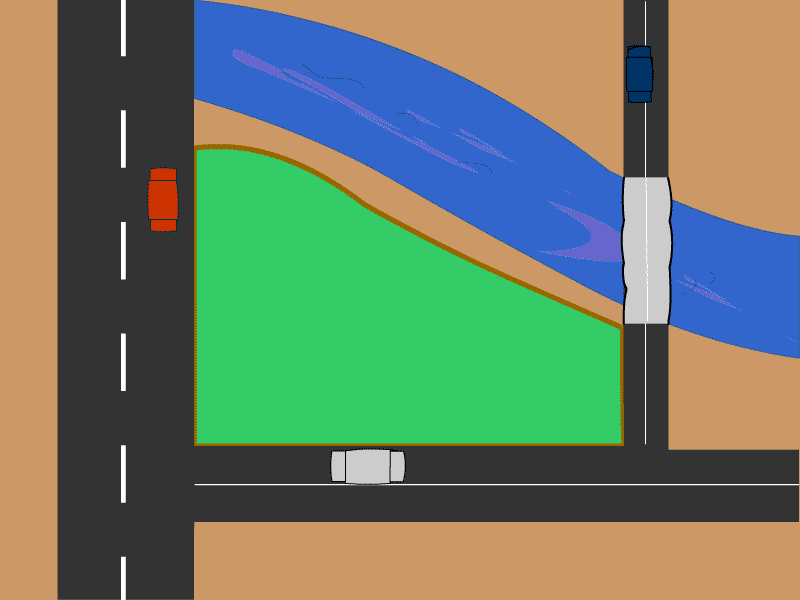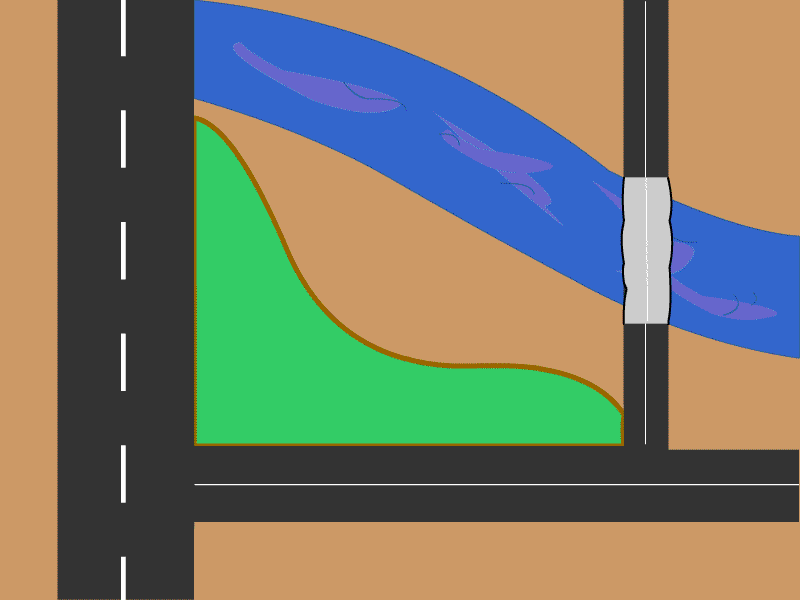
Figure 1. The boundary of the farmer's green patch is to be minimised while retaining the value of its area to be A. [Courtesy: G. Bharathi]