Write down the Gateaux variation of R defined as follows, with respect to w(x).
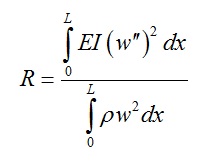
Given the potential energy, PE of a thin plate of arbitrary shape and thickness t and plate modulus D with a distributed transverse pressure load of q(x), obtain the governing differential equation along with the boundary conditions. Write and interpret ALL possible boundary conditions. E is the Young's modulus and nu is the Poisson's ratio of the material.
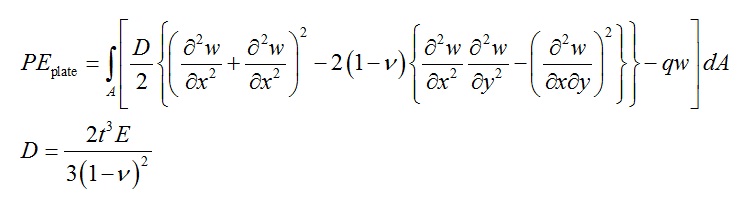
A chain of length L with m as the mass per unit length is hung in the presence of Earth's gravity between two points with coordinates (0,a) and (b,c). Write down the calculus of variations for this problem and solve it analytically and numerically. Assume some numbers. Interpret the Lagrange multiplier in this problem from the physics of the problem after obtaining an analytical expression for it.