Take two points A and B with coordinates (0,10) and (10,0) in the x-y plane. Assume that there is gravity along the y-axis. Find the circular arc passing through A and B such that a mass released at A with zero velocity slides down the arc to B in minimum time. Show that your answer satisfies the necessary and sufficient conditions. Extra credit for solving it analytically where A and B have coordinates (XA, YA) and (XB, YB).
Give a function in two variables (x,y) that has a "monkey saddle point". Draw the surface represented by the function using Matalb's "surf" command. Show also the contours of the function.
Shown in Fig. 1 is a four-bar linakge loaded by a spring of spring constant, kl. Its effect can be balanced by adding two springs, kb and kt. The three springs are "zero-free-length" springs in the sense that they exert a force proportional to the distance between their two ends. When the two ends are coincident, i.e., when the length is zero, they exert zero force. If the three relationships shown in Fig. 1 are satisfied, the four-bar linkage will have constant potential energy (here, that is also equal to the sum of the strain energies of the three springs) in all its configurations. Here, we have one parameter to choose: we can locate point H anywhere along the line KA extended beyond A. Your task is to find the location of H such that the potential energy is the least. Does such a minimum exist? Show details. Choose any four-bar linakge, the location of point K and the value of kl for numerical purposes.
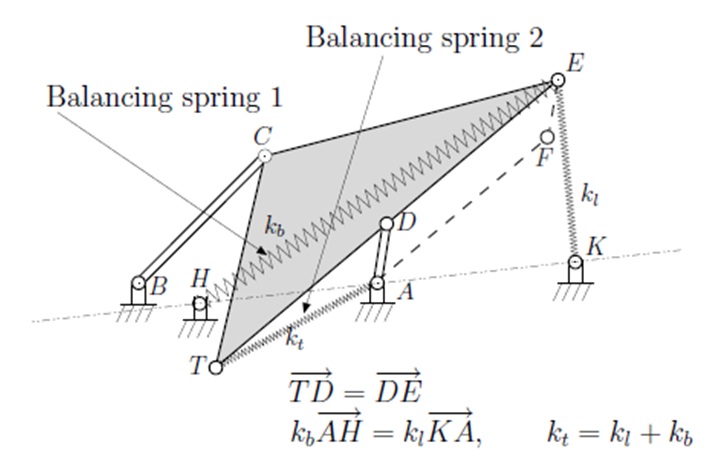
Figure 1. A statically balanced spring-loaded four-bar linkage with two other springs (Image from the PhD thesis of Sangamesh Deepak)
Extra credit for writing the simulation program to animate the four-bar in different positions along with the springs as well as a plot of the computed potential energy.
To help with the analysis of the four-bar linkage, you may use Freudenstein equation (Eq. (3) in this paper).