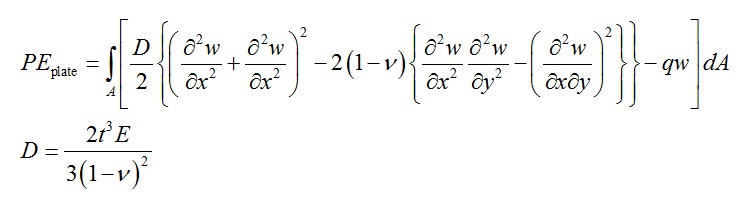Homework #4
Assigned: Feb. 19, 2013
Due: Feb. 26th, 2013
Points: 80
Additional points for work that is beyond instructor's expectation!
Look up Homework #1 of 2010 offering of this course and the solution posted there to know what is meant by "beyond instructor's expectation".

1. 30 points
   Take Gauteux variation of the following functionals. And then, Write the Euler-Lagrange-Ostrogradski equations and the boundary conditions for the following problems.
   
2. 10 points
   
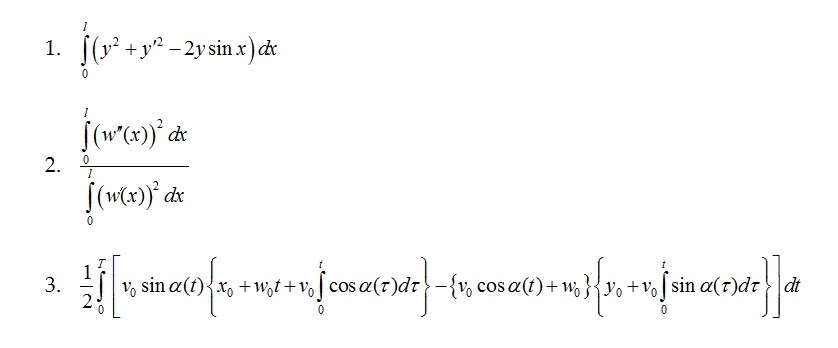
   Let a functional J be equal to the product of two other functionals K and L, all of which have the same domain. Show that variation of J is given by (K*variation of L + L*variation of K) for an arbitray vector h that is used to take the variation.
3. 40 points
   Write the boundary conditions that ensue when we minimize an intergral whose integrand depends on a function z(x,y) and its derivatives, z_x, z_y, z_xx, z_yy, and z_xy.
   Now take the potential energy expression for a plate and write the general boundary conditions.