Research

Underlying themes
Conventional principles in solid and structural mechanics invariably consider the onset of nonlinearities and instabilities to be failure modes. While this perspective continues to prevail in the context of material failure, our research on the mechanics of slender elastic structures is motivated by an emerging paradigm that seeks to exploit geometric nonlinearity as a functional principle for realizing novel engineering applications. The mechanistic principles we explore enjoy two distinctive features. First, by virtue of being dominated by aspect ratios rather than by absolute length scales, they are applicable across multiple length scales and can therefore be used, say, to design graphene nanostructures, create handy robots, or plan long-distance underwater cable layouts. Second, although displacements and rotations are typically large, the accompanying strains remain small and well within the proportional limit for elastic behavior. Hence, these principles enjoy near-complete independence from the material constitution. With this motivation, we are systematically addressing challenges in this rapidly growing field by adopting a comprehensive approach encompassing experimental techniques, mechanical modeling, numerical simulations, and novel applications.

Mechanics of elastic ribbons. Ribbons are slender structures characterized by three disparate geometric dimensions: length, width, and thickness, which are ordered such that length » width » thickness. The pair of aspect ratios length/width and width/thickness dictate their rich buckling-dominated mechanical behavior, and in turn, their widespread application- in miniaturized electronics or kirigiami-inspired structures, for instance. Their physical appearance suggests modeling ribbons as narrow elastic plates/shells, or as rods with highly anisotropic cross-sections, which closely parallels the dichotomy of approaches prevalent in the literature. Hence, ribbons are commonly modeled as von Karman plates or as Kirchhoff rods. Through carefully designed experiments and detailed numerical simulations with annular ribbons, we have demonstrated qualitative and quantitative deficiencies in these theories for modeling ribbon-like structures. 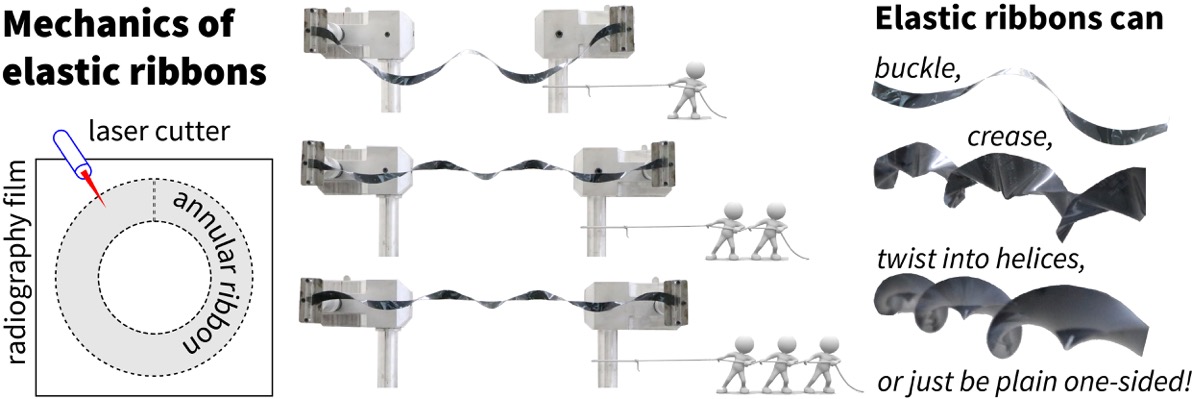Instead, we identified and validated, seemingly for the first time in the literature, the 1-director Cosserat plate model for elastic ribbons over a useful range of boundary conditions. In the process, we demonstrated annular ribbons to be prototypical systems for studying the mechanics of elastic ribbons. Annular ribbons exhibit a tunable degree of nonlinearity in response to simple boundary conditions, show multiple stable equilibria, bifurcation phenomena correlated with the number of zero crossings in the mean curvature, symmetry-breaking, and localization of energy.

Programmable control of Elastica robots. An emerging class of robots is composed of flexible structures that function by exploiting the compliances of their constitutive elements. Such robots are aimed at applications that demand high maneuverability for navigation in closed or cluttered environments, that require interaction with compliant substrates, and at applications where energy efficiency is critical. Their operating principle stands in stark contrast to traditional robots, which are typically composed of networks of limbs with actuated joints whose compliances are considered to be a hindrance for controlled operation. In this context, we have proposed and validated a mechanics-based approach to manipulate the (slow) planar motion of flexible elastic arms by controlling tensions in cables attached to its centerline. By adopting a geometrically nonlinear elastic model for the arm, by carefully accounting for configuration-dependent tendon loadings, and by interpreting the problem of manipulating the tip location or shape of the arm as a problem of load optimization, we demonstrated that it is possible to achieve a high degree of accuracy. Our novel control strategy represents a clear departure from conventional approaches for control in robotics. For instance, control is based solely on a predictive mechanistic model and is devoid of any sensory feedback. The resulting slender, remotely actuated, energy-efficient, and miniaturizable robot promises to serve as a prototype for applications in space robotics and robot-assisted surgery.

Computer vision techniques for experimental mechanics. The plethora of mechanical models for slender elastic structures stands in stark contrast to the scant availability of detailed experimental validation. Besides system-specific challenges, a common underlying difficulty stems from the complex and three-dimensional nature of deformations realized in these structures in response to simple loading conditions. Displacements are large, rotations are finite, and practically observed configurations lie far into post-buckled regimes. These considerations rule out correlation-based imaging techniques for measurement. Contact based shape measurements are invasive because of the small stiffnesses of slender structures. In this context, we have proposed novel computer vision techniques for sampling shapes and displacement fields of highly deformable structures. The essential idea underlying these contributions consists of designing robust strategies to resolve the correspondence problem in stereo triangulation. In particular, our marker-based and structured light imaging techniques yield Lagrangian and Eulerian descriptions of deformation. The latter technique inspired a graph-based algorithm that resolves a long-standing scan-to- CAD problem in surface reconstruction, albeit in the context of structured light imaging. The algorithm yields robust and automatic reconstruction in the form of parametric surfaces, and therefore promises to be useful in varied applications, including metrological inspection, e-commerce, and digitized artifact preservation.

Numerical agorithms for moving boundary problems. A important class of problems of interest in engineering involve evolving geometries. Examples include fluid-structure interactions, phase transformations, crack propagation and shape/topology optimization. Numerically simulating such problems poses a plethora of challenges. We address the issue of discretizing simplicial meshes conforming to moving boundaries in finite element simulations. With geometries changing shape or topology at each time step or at each solution iteration, such simulations offer no scope for manual intervention or heuristics. The idea of universal meshes is a promising prospect. Our work on analyzing guarantees for robustness and our software libraries providing efficient computer implementations represent a promising start. We believe that more interesting developments lie ahead- from permitting a richer class of geometries to exciting applications.