Publications
Google Scholar

How do you measure the shape of a Möbius strip?
We propose novel stereovision based techniques to answer this surprisingly overlooked question. Our measurements help critically evaluate the predictive capabilities of various mechanical/geometric models. The technique promises to be a useful alternative to DIC to digitize small-strain deformations involving large displacements and rotations.
A Kumar, P Handral, D Bhandari, R Rangarajan
Proc. Royal. Soc. A, 477 (2021), pdf
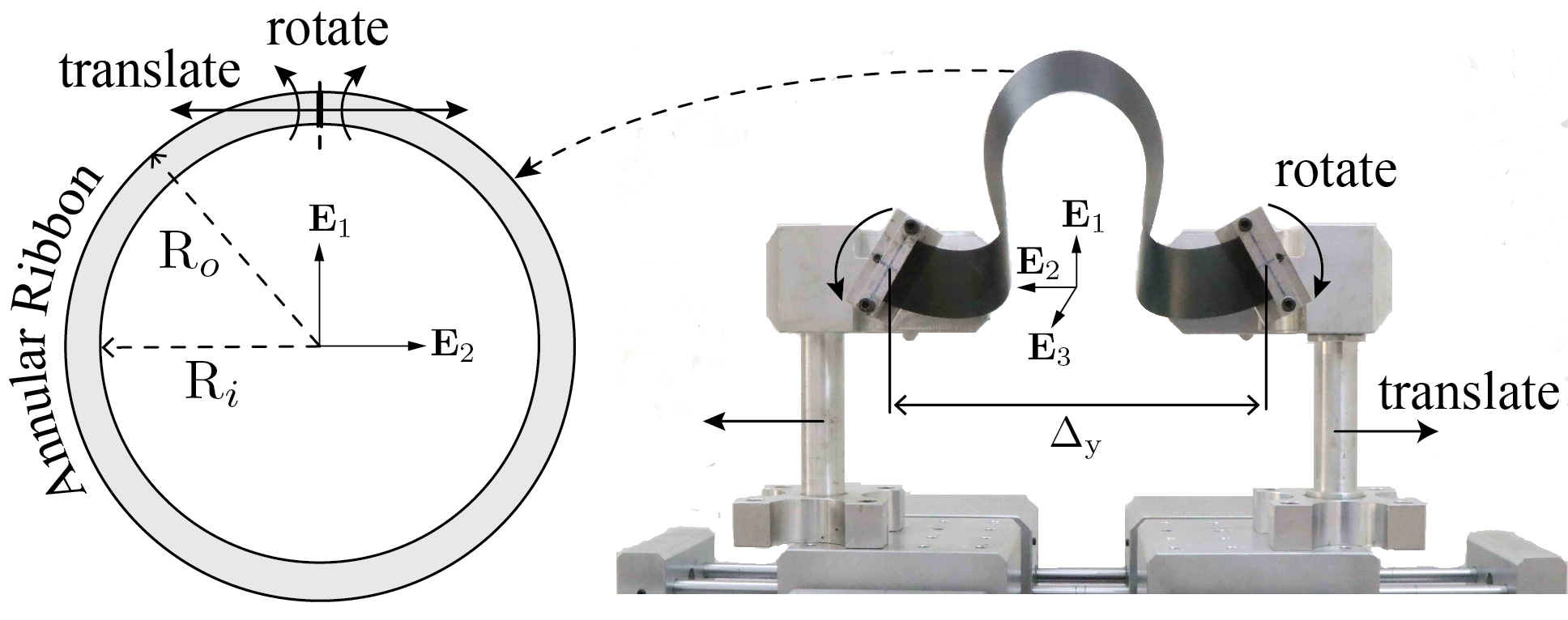
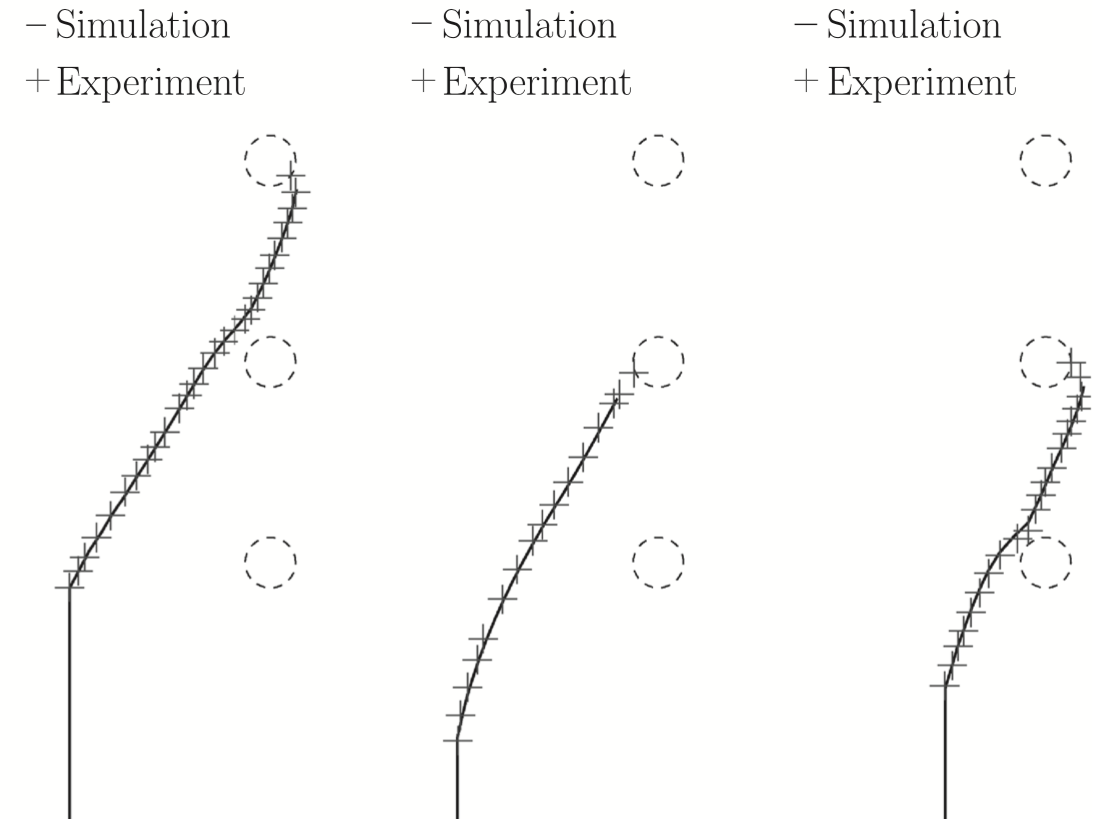
What is a good model for elastic ribbons?
Should they be modeled as plates? As rods? We use simple experiments and detailed numerical simulations to examine different modeling approaches.
A Kumar, P Handral, CSD Bhandari, A Karmakar, R Rangarajan
J. Mech. Phys. Solids, 143 (2020), pdf
, video

Can a flexible beam function like a robot?
Yes! We show that it is possible to programmatically control the tip motion of a planar flexible arm using just a pair of cables. Say hello to a 2D spring.
Features- ~1 mm accuracy for a 600 mm arm, light-weight, compliant, energy-efficient, low-cost
Featured on IISc’s front page!
P Handral, R Rangarajan
Extreme Mech. Letters, 34 (2020), pdf
, video
M&C lab’s first foray into releasing open source software!
Efficient thread-parallel C++ library for simplicial mesh improvement, implementing the provably robust directional vertex relaxation algorithm.
Benchmarks against Gmsh, NetGen, CGAL, Hypermesh.
Try it out!
R Rangarajan, A Lew
J. Open Source Software 5 (2020), pdf

Registering datasets (point clouds, curves, meshes, surfaces) to a common coordinate system requires ideas more than ICP. We propose, prove and demonstrate use of exponential coordinates and optimization on SO(3) for registration.
A Paman, R Rangarajan
Comput. Graphics Forum 38(2019), pdf

An unconventional approach to the obstacle problem. Typical simulations of contact compute the displacement field as the primal unknown. Instead, we compute the contact set as the primal unknown by adopting a shape-optimization approach.
Features- sub-meshsize accuracy for the contact set, no inequalities, no pressure-based tolerances.
A Sharma, R Rangarajan
Int. J. Numer. Meth. Engng. 117 (2019), pdf

A long-standing problem in numerical methods for moving boundary problems is the issue of meshing domains that change shape or topology frequently. This is the case in fluid-structure interaction or shape optimization problems, for instance. Remeshing at each time instant or solution iteration is riddled with issues. We propose the idea of universal meshes as a way forward.
R Rangarajan, H Kabaria, A Lew
Int. J. Numer. Meth. Engng. 117 (2019), pdf
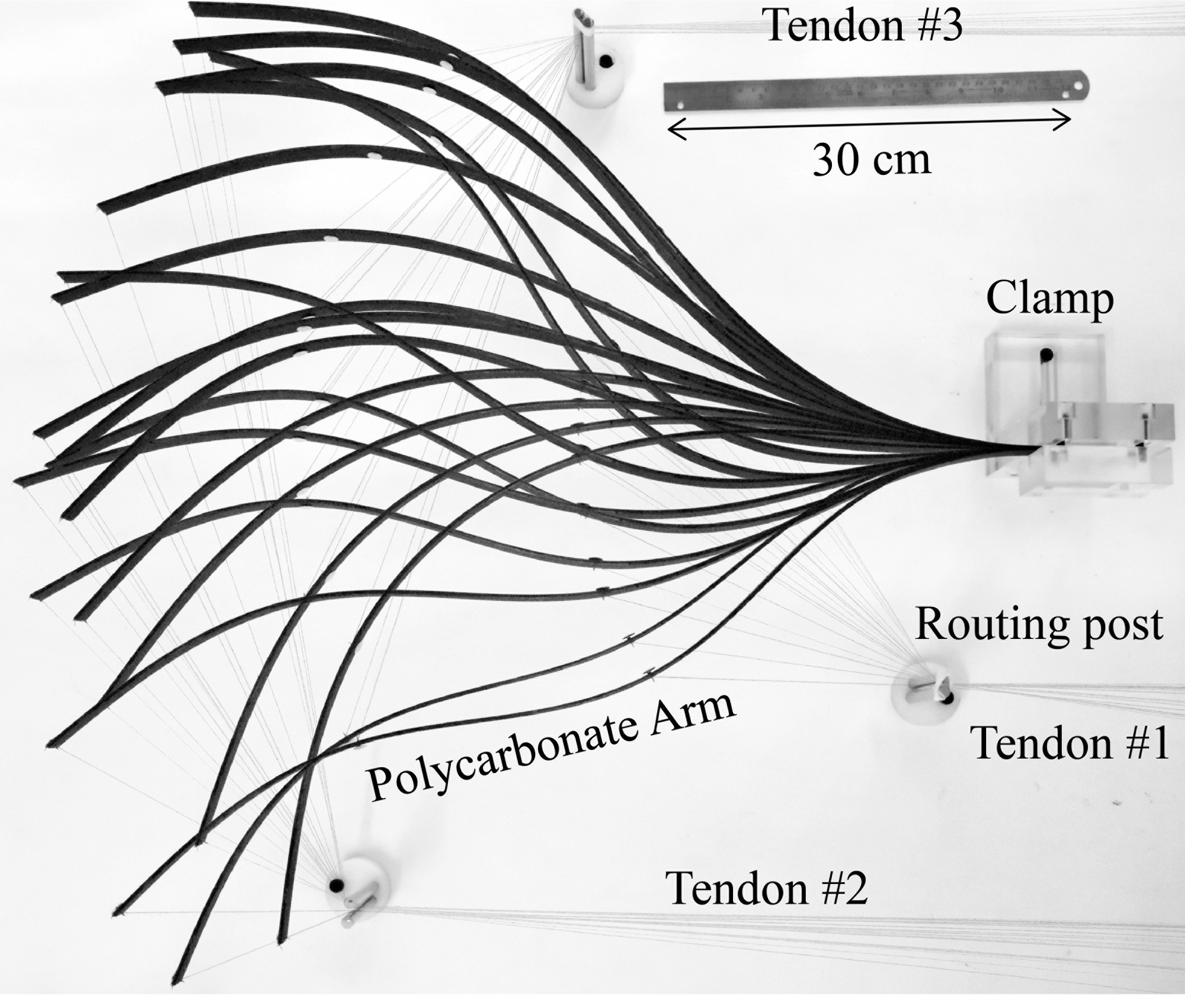
How well can we control the shape of a flexible elastic beam?
Quite well, using just a few cables. We formulate an optimization-framework for the inverse shape-control problem and demonstrate its performace. All mechanics, not AI/ML (yet).
A Nayak, P Handral, R Rangarajan
J. Applied Mech. 86 (2019), pdf

Minimax problems come up in varied scenarios. Our motivation to study it stems from a problem in mesh improvement- maximize the poorest element quality. We exploit reasonable assumptions on (quasi)-concavity of quality metrics to efficiently handle non-smoothness of the problem, and to construct a provably correct resolution algorithm.
R Rangarajan
Computational Optim. and Appl. 68 (2017), pdf
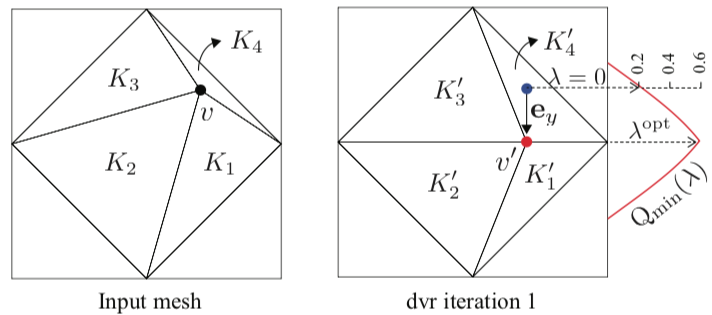
Strategies for mesh quality improvement span a wide specturm of complexity. Crucially, many provide no guarantees of improvement. We propose an iterative connectivity-preserving algorithm for improving qualities of simplicial meshes. With reasonable assumptions on the quality metric, we prove existence, uniqueness and a specific notion of convergence of iterations.
R Rangarajan, A Lew
SIAM J. for Scientific Computing, 39 (2017), pdf

Unlike plates and shells, fluid membranes possess reparameterization symmetry. We propose a finite element method that accounts for this property and explore its application to predicting configurations of biological vesicles and simulating adhesive interactions of vesicles with drug particles.
R Rangarajan, H Gao
J. Comput. Phys. 297 (2015), pdf
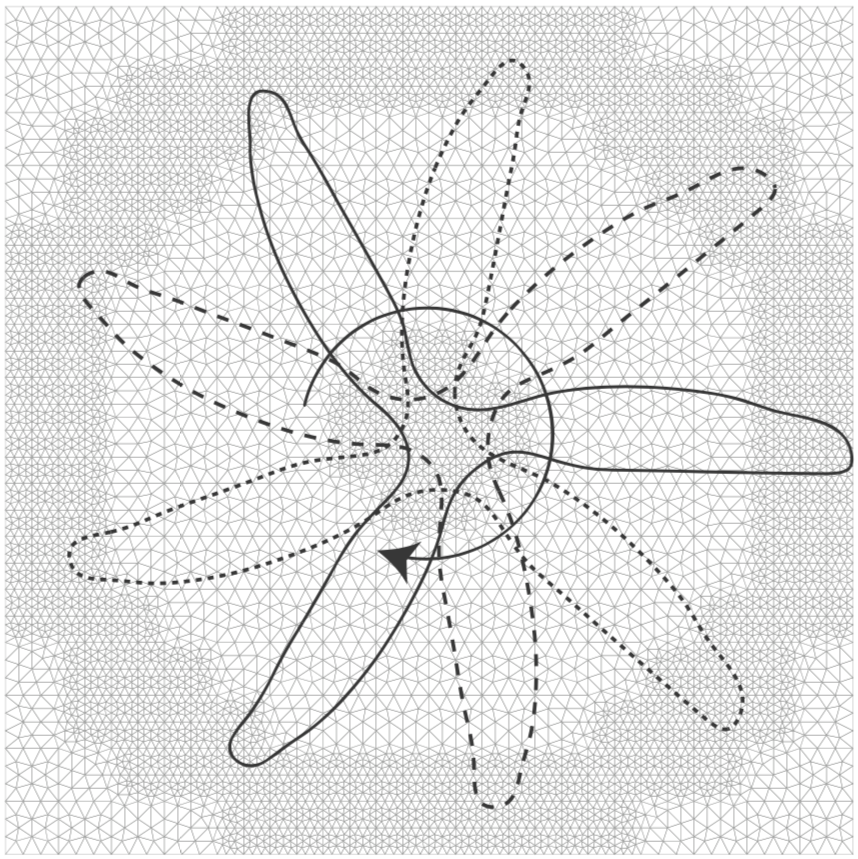
We simulate curvilinear fractures in brittle elastic materials. Two key ideas underlying the work- universal meshes to address the challenge of adapting the finite element mesh to a propagating crack path, and a special strategy to compute stress intensity factors accurately for curvilinear cracks.
5 authors, 5 countries of origin!
R Rangarajan, MM Chiaramonte, M Hunsweck, Y Shen, A Lew
Int. J. Numer. Meth. Engng., 102 (2015), pdf
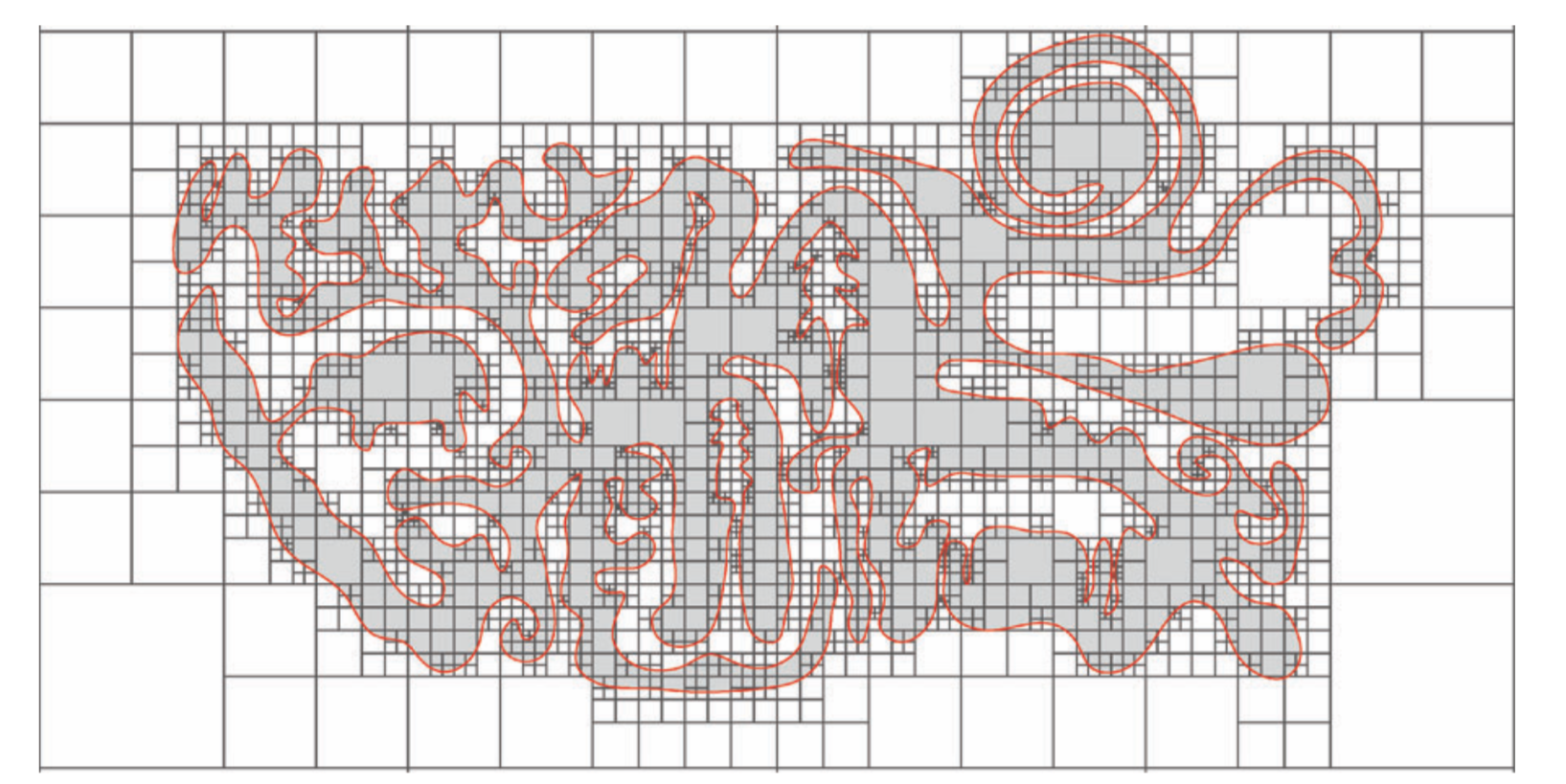
A new idea to handle evolving domains in finite element simulations
We demonstrate that it is possible to parameterize evolving geometries realized in numerical simulations over a subset of triangles in the same background mesh, called a universal mesh. In fact, we construct a homeomorphism provided that certain assumptions on smoothness of the geometry, and on angles and element sizes in the mesh hold. Furthermore, universal meshes enables designing high-order immersed boundary methods.
R Rangarajan, A Lew
Int. J. Numer. Meth. Engng., 98 (2014), pdf
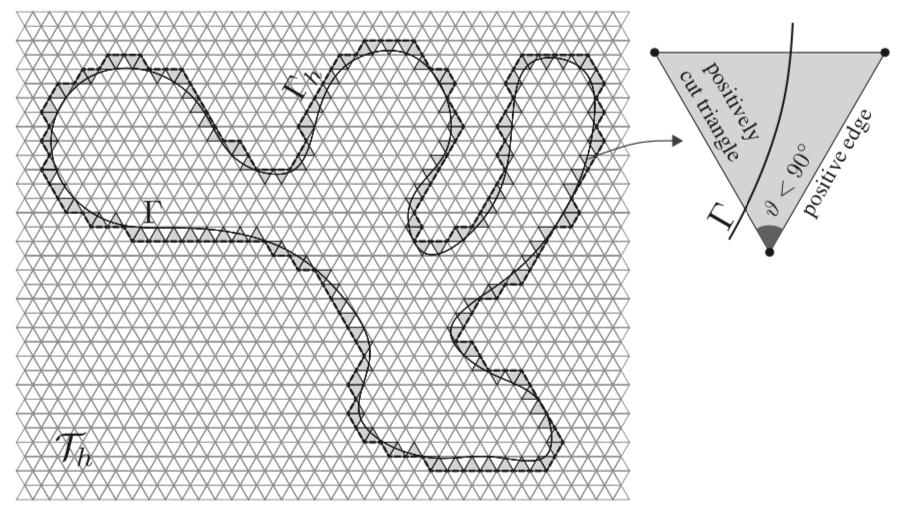
We prove that it is possible to parameterize curves over a select set of edges of a background triangulation using the closest point projection map. The analysis reveals that local restrictions on element sizes and angles can guarantee a global 1-1 map. The result is the basis of future explorations on universal mesh.
R Rangarajan, A Lew
SIAM J. Numerical Analysis 51 (2013), pdf
Demonstrating an idea to parameterize curves (cracks, boundaries, interfaces) over edges of a background triangulation. This enables constructing high order finite element spaces over curvilinear segments.
R Rangarajan, A Lew
Int. J. Numer. Meth. Engng., 88 (2011), pdf
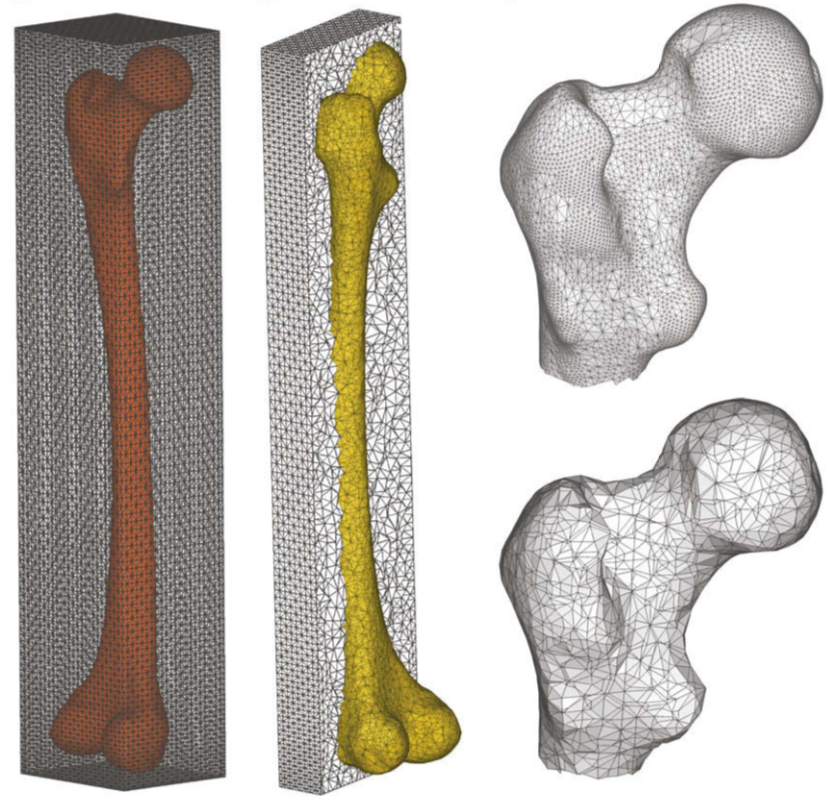
The combination of approximate discretizations for immersed geometries and strict imposition of Dirichlet boundary conditions leads to a problem of “boundary locking.” The finite element space can be over-constrained. We propose a non conforming finite element method to overcome the issue.
R Rangarajan, A Lew, G Buscaglia
Comput. Meth. Appl. Mech and Engng., 198 (2009), pdf

Simulating projectile impact on ballistic gels can provide useful information for armor design. Easier said than done. The short article discusses simulations incorporating asynchronous time integrators, local remeshing, mesh-to-mesh state transfer and numerical dissipation techniques.
R Rangarajan, R Ryckman, A Lew
Defense Tech. Infor. Center, 2008, pdf
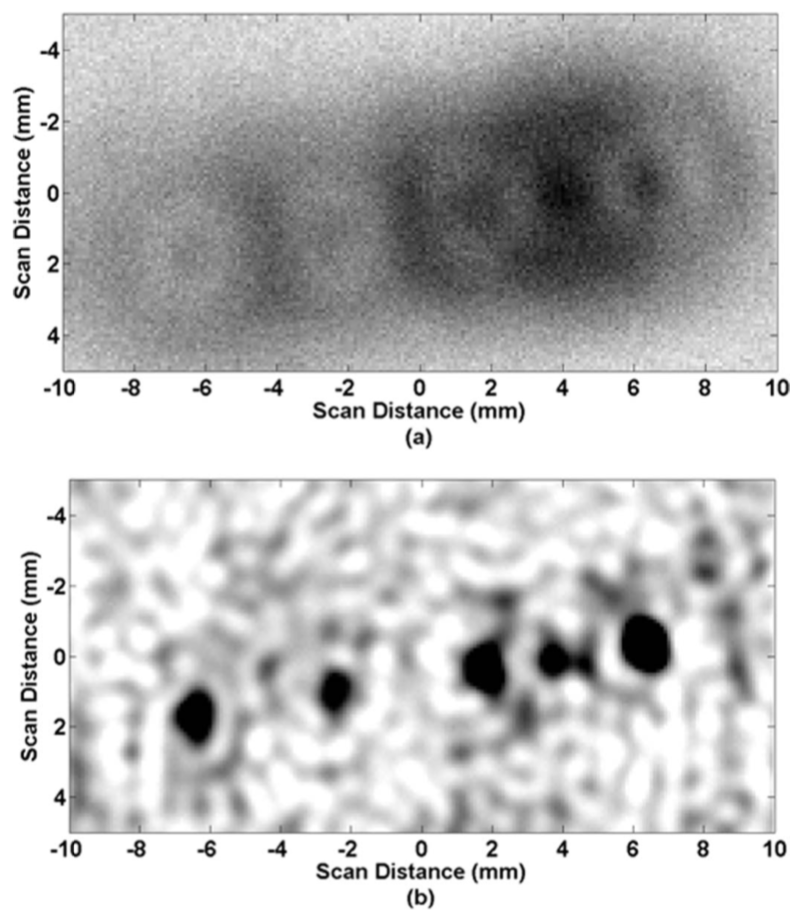
Scans using ultrasonic transducers are routinely used in non-destructive testing. But the recorded data is morphed by the signature of the transducer, namely, its point-spread function. This work proposes deconvolving experimental scans using computed point spread functions. Roughly speaking, like deblurring a foggy lens. We demonstrate accurate identification of defects using the technique, that are otherwise undetectable in the raw data.
R Rangarajan, CV Krishnamurthy, K Balasubramaniam
IEEE Trans. Ultrasonics, Ferroelectrics, and Frequency Control 55 (2008), pdf
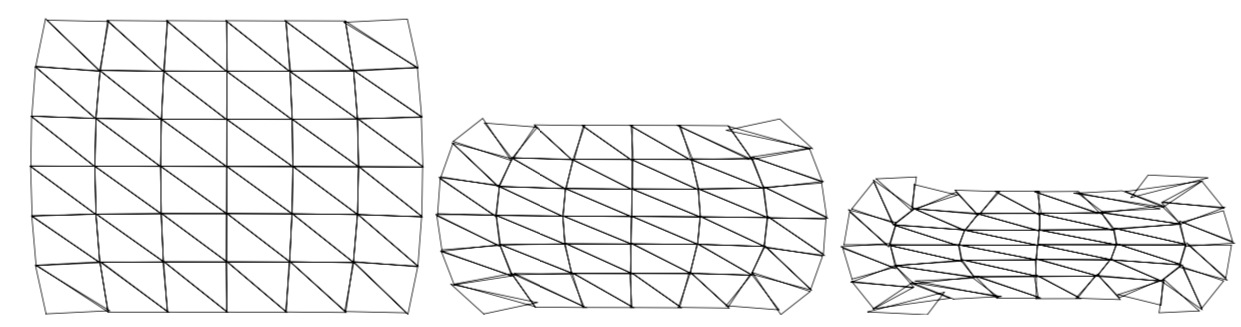
Discontinuous Galerkin methods provide algorithmic benefits in numerous scenarions. The short overview here discusses improved solution accuracy, handling of incompressibility constraints, and overcoming implicit mesh-based kinematic restrictions.
A Lew, A Ten Eyck, R Rangarajan
IUTAM Symposium on Theoretical, Computational and Modelling Aspects of Inelastic Media (2008), pdf