Mechanics of Solids and Structures
Mechanics of solids caters to a longstanding interest of the Department, spanning multiple scales (macro to micro) and multiple domains (fracture, MEMS, biomechanics). Work in this broad area includes analytical, computational, and experimental research projects. Prof. K.R.Y. Simha studies fracture in thin-film coating, dynamic loading on plates and shells for impact-resistant shields, and more recently, fracture in friction-stir welded joints. Prof. R. Narasimhan’s group has been actively involved in analytical, experimental and computational studies on crack-tip fields and void growth in ductile face-centered cubic (FCC) single crystals. These investigations have established the structure of these fields for different lattice orientations, constraint levels and fracture configurations. He has also been working on the role of several factors such as pressure-sensitive yielding, internal friction, flow softening, Poisson’s ratio and mode-mixity in the fracture response of bulk metallic glasses (BMGs). Prof. C.S. Jog has made substantial strides on the formulation of the finite element method with the implementation of hybrid elements, wherein displacement and stress are independently interpolated for computational benefits in multiphysics simulations.
In addition to extensive research in fracture and computational mechanics, recently a number of faculty are exploring other aspects of solid mechanics. Prof. Namrata Gundiah is engaged in experimental and computational work in biomechanics of tissue and cells. She has also studied the mechanics of insect boring. Prof. Ramsharan Rangarajan conducts research aimed at probing the role of geometry in slender structures such as beams, ribbons, and shells. Prof. G.K. Ananthasuresh’s group studies mechanics-based design of compliant mechanisms, growth modeling in plant leaves and inverse problems in elastic mechanics. His group has ongoing work in multiple pathways in bistable arches and shells with innovative designs of devices that exploit this feature.
Computing shapes through optimization
Ramsharan Rangarajan
A common theme uniting problems of shape optimization in structural design, crack propagation in solids, and phase transformation during melting, is the fact that a principal unknown is a shape – a domain, a crack and an interface, respectively, in the three examples just mentioned. These are in fact instances of free and moving boundary problems. Such problems that require a shape to be computed as part of the solution pose a conundrum to conventional simulation methods that typically start with a geometry and discretize it to resolve a set of equations: where to start and how to proceed?
Prof. Rangarajan’s group is working on designing robust numerical algorithms to answer precisely these questions. In recent work, it was demonstrated that certain scenarios of contact between elastic membranes and rigid obstacles can be posed as a problem of optimizing the shape of the contact interface. This offers the benefits of accurately estimating the contact region and avoiding the need for including any inequalities or constraints when computing solutions.
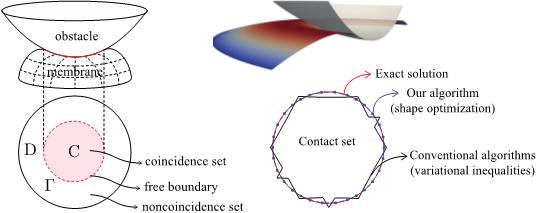
An example demonstrating a novel algorithm that treats contact as a free-boundary problem.
Modeling, simulating and measuring shapes of buckled ribbons
Ramsharan Rangarajan
The influence of geometry in structural mechanics is perhaps most evident in buckling phenomena. Such geometrically nonlinear behavior is not anomalistic but the norm in the mechanics of slender elastic structures. Current research in the group is focused on modeling quasi-static deformations of elastic ribbons. A key aspect of this effort consists in comparing model predictions with experimental measurements. Th e group is working on novel computer-vision based techniques to noninvasively measure large 3D displacements observed in experiments.

Qualitative comparisons between measured and simulated shapes of annular elastic ribbons undergoing large displacements and rotations
Mechanics of Soft Matter
Namrata Gundiah
Research interests in Prof. Gundiah’s lab mainly lie in the broad areas of tissue mechanics, mechanobiology and biomaterials. At the scale of tissues, she uses methods in nonlinear mechanics, viscoelasticity, and poroelasticity to quantify the properties of naturally occurring biomaterials and those fabricated using synthetic polymers. The role of elastin, a rubber protein in vertebrates, has been a main area of interest in her laboratory. In earlier studies, it was shown that arterial elastin displays a nonlinear rubber-like mechanical response which may be better described using constitutive models that incorporate orthotropic material symmetries to account for elastin layout. These results were among the first to measure the biaxial mechanical properties of elastin networks isolated from vertebrate arteries.
More recently, work from her lab, using a composite nonlinear mechanics framework, delineates the individual contributions of elastin and collagen to the mechanics of arterial tissues in healthy and diseased conditions. Results show age-dependent mechanical response of human ascending thoracic dissections which suggests the importance of stretch-based homeostasis in tissue remodeling in the arterial media.
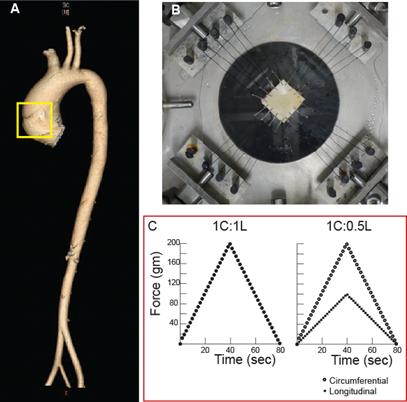
(a) Aneurysm and dissection in human ascending aorta, (b) planar biaxial testing instrument used to characterize arterial tissues and (c) results from force-controlled biaxial and non-equibiaxial experiments (Babu et al., J. Biomech. Eng., 2015).
Ongoing investigations are aimed at quantifying the mechanics of dissections in arterial tissues using peel studies. In other studies, her group has also demonstrated the importance of entanglements and cross-links in the material properties of poly-di-methyl siloxane networks. Using scaling laws in polymer physics, in combination with dynamic mechanical analyses, the influence of crosslinking density, solvent, and sol f raction in network properties is demonstrated. Her group is also involved in the fabrication and mechanical characterization of hydrogels such as silk, gelMA, conducting polymers, and gelatin-elastin scaffolds which are important in tissue engineering.
Mechanics of substrate boring by insects
Namrata Gundiah
Materials in nature generally have specific functional attributes; for example, parasitoid wasps must overcome several mechanical constraints to successfully deposit eggs. These begin with selection of suitable substrates through which the ovipositor penetrates without itself fracturing. The insect must next steer and manipulate the ovipositor to deliver eggs at desired locations and finally retract her ovipositor fast to avoid possible predation. This process is repeated multiple times during her lifetime. Because parasitoid ovipositing behavior involves active interactions of the ovipositor with the substrate, it poses fascinating questions from a materials perspective. Specifically, what are the mechanisms that parasitoid insects use to bore through substrates of variable stiffness? What are the properties of the ovipositor and methods used to reduce material wear and increase toughness? These questions have been addressed to demonstrate novel mechanisms of the tools used by insects to cut through hard substrates. On examining different structures within the insect-wing hinge, a clutch-gear mechanism is shown to enable insect flight.
More recent work has quantified the biomechanics of cutting by beetle mandibles; these mouth parts of the insect have zinc enrichment at the substrate cutting edges which is linked to its increased material hardness. Using a fracture mechanics framework, a scaling model is developed for the cutting of coffee wood by wood-boring beetle mandibles to link mandible shape and properties in the generation of small wood chips suitable for ingestion. Biomimetic studies to link such interactions provide unique insights which may be useful in engineering from the perspective of tool development.

a) Highly curved ovipositor of fig wasp parasitoid, (b) Scanning electron micrograph of ovipositor shows teeth-like structures enriched with zinc (c and d) Chemical and mechanical sensillae located on the ovipositor (Kundanati and Gundiah, J. Exp. Biol.).
Computational Mechanics of Solids
C.S. Jog
Contact mechanics problems are among the most challenging problems in the area of computational mechanics. The contact area is not known apriori and needs to be determined as part of the solution along with the other field variables. Prof. Jog’s group is currently working on developing contact formulations within the context of hybrid finite elements. Hybrid finite elements are based on a two-field variational formulation involving independent interpolation of the displacement and stress fields. They are known to significantly reduce the problem of locking that plagues standard displacement-based formulations. Besides the hybrid formulation that allows a significant improvement in coarse-mesh accuracy, a new pressure projection scheme has been developed that is particularly cost-effective and removes the spurious oscillations that occur in the p ressure field with the conventional strategy. The proposed hybrid strategy along with the pressure projection scheme shows significant advantages over conventional formulation especially in analyzing contact of shell-type structures.
Fracture Mechanics
K.R.Y. Simha & R. Narasimhan
The unification of fracture mechanics concepts via experimental, theoretical and computational models have become the mainstay for assessing structural safety and reliability on one hand and for designing novel fracture testing methods on the other. A novel idea for designing a constant form factor edge-cracked semi-circular compression disk specimen was tested by Prof. Simha’s group and calibrated for extending fracture testing to deal with thin film and coatings. Brittle fracture almost always occurs suddenly; and, therefore, modeling impact and stress wave propagation in solids and structures assume importance. Prof. Simha’s group has been active in modeling dynamic loading on plates, shells, tubes and honeycombs to enable designing blast and impact resistant shields for defense and space applications. There is a great need today for reinstating the primacy of basic physics and mechanics to aid advanced materials and manufacturing including bimetallic strips, single crystals, bulk metallic glasses and 3D printed objects. A preliminary investigation on residual stresses generated in friction stir welded dissimilar metallic joints is under progress.
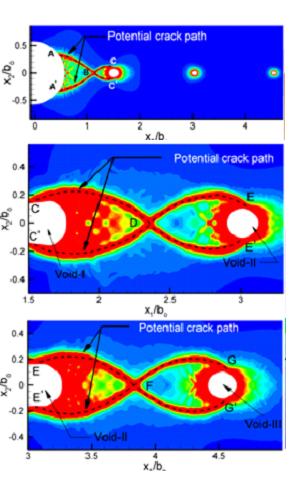
Prof. Narasimhan’s group has been performing analytical, experimental and computational studies on crack tip fields and void growth in ductile FCC single crystals. These investigations have established the structure of these fields for different lattice orientations, constraint levels and fracture configurations. This can guide the choice of texture and microstructure of polycrystalline alloys which will display higher fracture resistance. Ongoing research in this area is focused on failure of magnesium alloys (HCP) which deform plastically by a combination of crystallographic slip and twinning. An important contribution of this work is to establish the role of {10-12} twinning (extension twinning) on dissipation and toughening. The results have provided new insights on the mechanics of fracture of FCC alloys and Mg alloys from the perspective of individual grains.
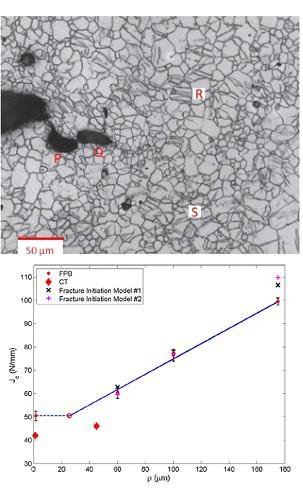
Void growth and coalescence ahead of a crack tip in AZ31 Mg alloy. (b) Notched fracture toughness versus notch rot radius obtained from experiments along with predictions from two fracture initiation models based on Rice-Johnson and Rice-Tracey theories (Prasad et al., Engg. Fract. Mech., 2018).
In a very recent study, the effect of notch root size on the fracture behavior of AZ31 Mg alloy was investigated through experiments performed with notched 4-point bend specimens. The results showed a change in fracture mechanism from twin-induced cracks (quasi-brittle) to void growth and coalescence by internal ligament necking (ductile) with increase in notch root radius. The fracture toughness increases dramatically with notch root size. This trend is closely predicted using simple void growth and coalescence models based on Rice-Johnson and Rice-Tracey theories.
Professor Narasimhan’s group has also been working on the role of several factors such as pressure-sensitive yielding, internal friction, flow softening, Poisson’s ratio and mode-mixity on the fracture response of bulk metallic glasses (BMGs). It has been shown through careful experiments that ductile BMGs fracture by a fluid meniscus instability mechanism occurring inside a dominant shear band at a notch tip (see Fig.2). For the first time, the fracture process zone length over which the above mechanism operates has been measured and related to the stress distribution ahead of the tip by combining the experimental results with finite element simulations.
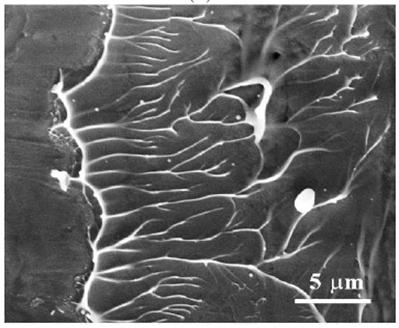
Taylor-Saffman fluid meniscus instability mechanism operative on fracture surface of a Zr-based BMG (Tandaiya et al., Acta Materialia, 2013).
Experimental studies have shown that nano-corrugations form on the fracture surface of brittle BMGs. Although several mechanisms have been proposed in the literature, none of them is supported by fundamental physics-based theories or simulations. Prof. Narasimhan’s group has recently demonstrated through continuum simulations that brittle BMGs fracture by spontaneous nucleation of multiple cavities which coalesce via dynamic crack growth along curved shear bands.
Finite element simulation results of plastic strain showing (from top to bottom) (a) spontaneous cavitation ahead of a crack tip in a brittle BMG and (b,c) their coalescence via curved shear bands giving rise to nano-corrugations (Singh et al., PRL, 2016).
BMGs exhibit negligible ductility under tensile loading and fail by unstable propagation of a single dominant shear band. Among the strategies that are being explored to enhance their tensile ductility, one of the prominent ones is to use bulk metallic glass composites (BMGCs) which have soft crystalline phases interspersed in the amorphous matrix. However, only few mechanics-based studies have been undertaken to investigate their mechanical response. Continuum finite element analyses are being performed to ascertain the role played by the volume f raction (Vf) and strain hardening behavior of the crystalline reinforcements on the strength and ductility of BMGCs. These simulations have shown that highly strain-hardening elongated dendrites with Vf ~45% would make the BMGC ductile without any penalty on the strength. Thus, these results provide design guidelines for strong yet ductile BMGCs.
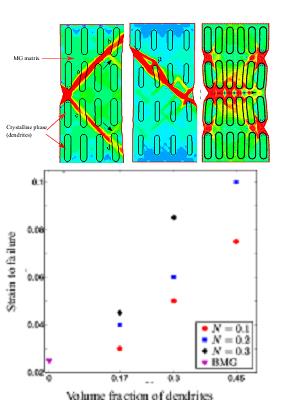
Contours of plastic strain in BMGC showing shear bands blocked/deflected by dendrites for (a) Vf = 30%, low hardening, (b) Vf = 17%, high hardening and (c) Vf=45%, high hardening. (d) Critical strain at failure versus volume fraction of dendrites for different hardening exponents (Shete et al., Scripta Materialia, 2016).
Mechanics, Optimization, and Stability of Structures
G.K. Ananthasuresh
The research group of Prof. Ananthasuresh is interested in compliant mechanisms, which are structures that elastically deform with large displacements but small strains. This work combines mechanics with structural topology optimization, synthesis, and inverse problems and focuses on numerous applications in cell mechanics, MEMS devices, biomedical devices, and high-technology product design. In the last five years, the topics pursued by this group include bistability of shallow arches, topology derivative, tensegrity structures, and mechanics of growth. To elaborate, their work has led to analytical and semi-analytical solutions to analyze and design bistable arches. A bilateral relationship between two stable arch-profiles was derived for shallow arches, which made designing arches straightforward and simple. Also studied is coupled flexural-torsional buckling of arches where the interplay among bending, axial, torsional, and warping energies is conveniently exploited for novel insights into the mechanics of arches. Topology derivative is an emerging concept wherein the low-order sensitivity of a performance functional is analytically derived using a generalization of the shape derivative and asymptotic expansion of the perturbed solution. This is being extended for introducing hole wi th Dirichlet boundary conditions for gainful application in designing structures that take advantage of additive manufacturing. An optimization-based tensegrity design is being applied to the design of a large (3 m diameter) space-antenna. Mechanics of growth is being pursued computationally and experimentally by considering leaves of plants and trees to discern the growth-rate tensor and the patterns of resultant growth.

High-speed videography to study multimodal bistability in arches.

Modeling of growth in leaves to compute the shape along with residual stress; an experiment on tobacco leaves to measure resultant growth and thereby compute the inherent growth.
